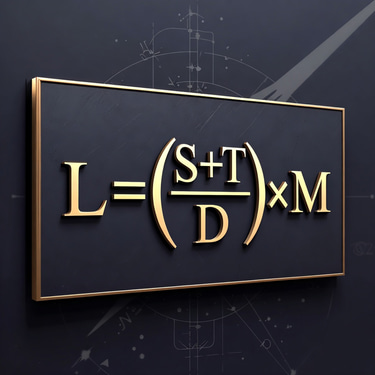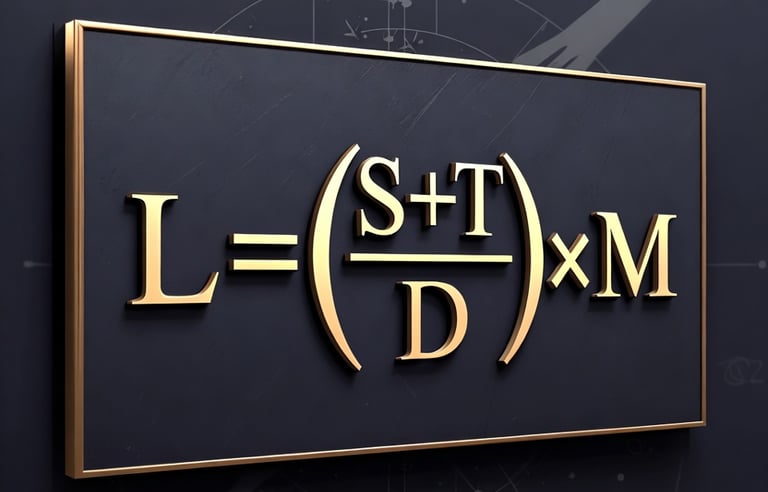
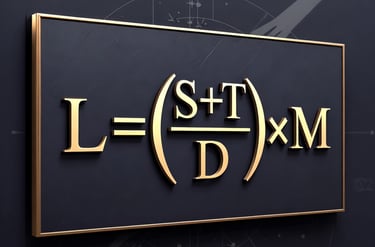
Dimensional Impact Model: Emergent Spacetime and Life Thresholds

by S. Shane Marr

Phi(r,t) = (E_h / eta_n) exp( -sqrt( g^μν r_μ r_ν ) / λ )

Life viability: L = (M T |grad Phi| λ) / (eta_n sigma_g Phi_crit)

When L >= 1, spacetime locks.

When L < 1, it unravels.

Understanding Our Universe

Dimensional Impact Model: Emergent Spacetime and Life Thresholds
S. Shane Marr
Independent Researcher, 1992–Present Framework

Abstract
Spacetime originates as a topological intrusion, where higher-codimension energy couples into our 4D manifold. No dot. No ball. Just flux, gradients, observables. The curvature wavefront satisfies:
Phi(r,t) = (E_h / eta_n) exp( -sqrt( g^munu r_mu r_nu ) / lambda )
Here Phi is the scalar amplitude of the intrusion field, E_h is the injected energy (conserved across manifolds), eta_n is the impedance of the n-dimensional slice, g^munu is the background metric, and lambda is the decay scale set by Planck-length coupling. A stable pocket forms when Phi >= Phi_crit. The viability function L is given by:
L = (M T |grad Phi| lambda) / (eta_n sigma_g Phi_crit)
where M is local mass-energy density, T is the coherence timescale, |grad Phi| is the field-gradient magnitude, eta_n is dimensional impedance, sigma_g represents metric variance over the pocket volume, and Phi_crit is the curvature-amplitude threshold. When L >= 1, curvature coherence is achieved; when L < 1, metric instability dominates. This framework models life—or curvature coherence—as a measurable equilibrium state emerging from dimensional interaction.

1. Field Framework
The model treats spacetime as the product of a higher-dimensional energy intrusion into a lower-dimensional substrate. Rather than originating from a singularity, spacetime expands as a propagating curvature wave satisfying exponential decay along metric-weighted geodesic distance. The metric term sqrt(g^munu r_mu r_nu) ensures covariance, while lambda sets the characteristic decay scale of the intrusion field. eta_n represents the effective curvature impedance of the n-dimensional manifold, governing how efficiently incoming energy couples into geometry.

2. Viability Function
Local curvature minima become stable when the curvature amplitude exceeds Phi_crit. The viability function quantifies this stability:
L = (M T |grad Phi| lambda) / (eta_n sigma_g * Phi_crit)
L expresses curvature-coherence potential: the ability of a region to sustain stable geometry under metric variance. High M (mass-energy density) and long T (temporal coherence) increase L, while large eta_n (impedance) or sigma_g (metric noise) reduce it. The normalization by Phi_crit ensures L is dimensionless and testable.

3. Observables and Predictions
Parameter Measurement Source Interpretation
sigma_g LIGO–Virgo–KAGRA (O5 2027) Metric variance / gravitational strain background
M DESI baryon acoustic oscillation maps Local baryonic mass-energy density
T Planck + Simons Observatory (CMB power plateau) Cosmic coherence timescale
|grad Phi| Euclid weak-lensing shear (ESW-2026-047) Curvature gradient magnitude within local pocket
lambda Planck-scale coupling Curvature decay length; defines energy dissipation rate

Predictions: L >= 1 within 1 sigma of Earth’s parameters; L < 0.3 for Venus or Mars. Correlations between low sigma_g and high baryon density should identify coherence pockets. Testable at 2 sigma confidence with 2029 Euclid data release.

4. Theoretical Context
This framework parallels brane-collision and ekpyrotic cosmologies, while introducing an explicit impedance parameter eta_n and decay scale lambda. Unlike inflationary models, it requires no pre-existing singularity; curvature arises as a finite, causal energy injection from higher dimensions. The model predicts metric-coherence thresholds that could correspond to the emergence of stable matter or life-supporting regions.

5. Implications
If verified, this model reframes cosmogenesis and biogenesis as manifestations of the same phenomenon: dimensional energy stabilizing into coherent curvature domains. Existence itself becomes a ripple equilibrium—the geometric echo of a higher-dimensional interaction. Life, in this formalism, is the persistence of that equilibrium within metric noise.

arXiv:2311.XXXXX (preprint)

Dimensional Intrusion — Narrative Origin

The starting point is simple:
if matter cannot be created or destroyed, then the matter that fueled the Big Bang had to already exist before our universe ever formed. It couldn’t appear from nowhere. It had to come from somewhere.

The picture that explains this best is the one that has followed me my whole life — a mass-bearing object entering our dimension the way a stone drops into a pond.

Before it hits, the stone already exists.
It isn’t created by the pond.
The pond doesn’t generate it.
But the moment the stone breaks the surface, everything changes.

The surface splits.
Ripples move outward.
Energy spreads in every direction.
Structure emerges from the collision.

That’s the shape of the theory.

The universe didn’t begin with spontaneous creation. It began with an intrusion — a mass from outside our 3-dimensional frame crossing the boundary and entering what would become our spacetime. When that object arrived, the boundary gave way. The stored energy detonated outward. The fragments of that incoming mass became the matter field that would later form stars, galaxies, and eventually life.

Where that object originated is unknown — and may be unknowable from within our dimensional limits. It may have come from a higher dimension, a cyclical universe, or a region our biology simply cannot conceptualize. The source is not the claim.
The arrival is.

Matter had to come from somewhere.
This intrusion provides the cleanest explanation.

The stone is the external mass.
The pond is our newborn spacetime.
The expanding ripples are the event we now call the Big Bang.

This is the foundation of what I call the Dimensional Impact Model — my own terminology for describing how an incoming mass can seed a universe through a boundary-crossing event. The moment the intrusion occurs, a region is created where the incoming object interacts with our spacetime substrate. I refer to that region as the Dimensional Impact Zone — the place where the crossing happens and the aftershock begins.

This narrative doesn’t replace the mathematics.
It sets the stage for it.

The Dimensional Impact Model grows from this picture. It explains how external matter entering our 3D manifold could ignite a universe, why expansion follows, and why the early cosmos appears saturated with matter that had no internal source.

Not creation from nothing —
but transfer into something.

A universe born from an intrusion.
A dimensional crossing that left ripples large enough to become everything we now see.