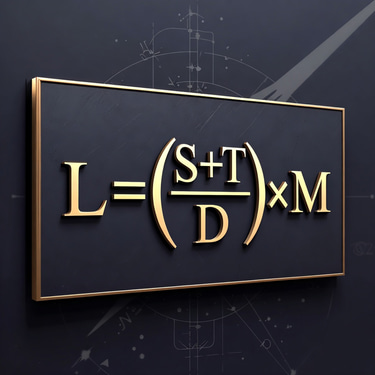The MARR Equation: A Unified Model for Life Viability Author: S. Shane Marr Version Tag: MARR Equation v1.0

Abstract

The viability of life has traditionally been assessed through fragmented models, from Einstein’s relativistic field equations describing spacetime geometry to the Drake Equation estimating probabilities of communicative civilizations. These frameworks either lack a direct life-sustainability criterion or treat critical factors as independent probabilities without penalty terms. The MARR Equation, introduced here, provides a unified viability index:

L = ((S + T) / D) * M

where S represents spatial support, T temporal stability, D dimensional cost, and M matter–energy presence. Life is postulated to emerge or persist only when L >= L_critical, a threshold empirically determined. This formulation captures additive contributions of space and time, imposes a penalty for hostile dimensional environments, and gates viability through material and energetic availability. Unlike purely probabilistic models, the MARR Equation yields a normalized scalar that can be calibrated against astrophysical observations, planetary data, and thermodynamic constraints.

This paper defines each variable formally, compares the model with existing theoretical constructs, and outlines pathways for calibration using exoplanetary catalogs and cosmological data. The MARR Equation is positioned as a testable, extensible framework for unifying cosmology, astrobiology, and quantum theory in the study of life viability.

Introduction

2.1 Background The question of where and how life can arise has driven scientific inquiry across physics, biology, and astronomy. Einstein’s general relativity formalized the link between mass–energy and spacetime geometry, but offered no metric for whether those conditions are biologically supportive. Astrophysical habitability studies have since focused on stellar placement, orbital dynamics, and geophysical cycles, while thermodynamics has emphasized entropy and energy gradients. In parallel, astrobiological models such as the Drake Equation sought to estimate the probability of intelligent life, but treated many factors as independent and probabilistic rather than structurally constrained.

2.2 Gaps in Existing Theories

• Einstein’s field equations describe geometry, not viability. They quantify curvature but do not directly map to the requirements of life.

• The Drake Equation is heuristic and probabilistic, with factors multiplied linearly and no structural penalty for hostile environments. Its scope is communicative civilizations, not the baseline emergence of life.

• Habitability indices (e.g., circumstellar habitable zone, continuous habitable zone) rely on specific astrophysical parameters but lack integration with temporal stability, dimensional effects, or energetic sufficiency.

• Quantum and cosmological theories have highlighted possible variability in time stability and dimensional structure, yet these influences remain unincorporated into models of life’s viability.

Thus, while individual theories quantify key ingredients, none provides a single scalar index of life-support potential that integrates geometry, time, dimensional penalties, and material–energetic requirements.

2.3 Purpose The purpose of this work is to propose and formalize the MARR Equation, a unifying model of life viability expressed as:

L = ((S + T) / D) * M

The equation provides a normalized viability index L, with the hypothesis that life emerges or persists only when L >= L_critical. By structuring additive support terms (space and time), a divisive penalty term (dimensional cost), and a multiplicative gating term (matter–energy presence), the model captures the minimal necessary conditions for life within a single framework. This paper defines each variable mathematically, situates the model against prior theories, and proposes paths for empirical calibration.

The MARR Equation

Formal Expression L = ((S + T) / D) * M

Where

• L = Life Viability Function — dimensionless scalar indicating whether conditions permit the emergence or persistence of life.

• S = Space Support Term — availability and stability of spatial conditions (habitable zones, planetary system stability, atmospheric retention).

• T = Time Stability Term — continuity of supportive conditions (duration of habitability, entropy rates, stability of physical constants).

• D = Dimensional Cost Term — penalty for dimensional complexity, curvature, instability, or hostile physics (e.g., compact-object proximity, high-curvature spacetimes, extra-dimensional leakage).

• M = Matter–Energy Presence Term — density, availability, and usability of matter/energy (chemical elements, free energy, radiation balance).

Critical Threshold Condition L >= L_critical Life can only exist or sustain when the computed viability exceeds a minimum critical threshold L_critical, to be defined via observational or theoretical calibration.

3.1 Variable Domains (Normalized) All terms are normalized so that L is dimensionless. Representative domains: S ∈ [0,1], T ∈ [0,1], D ∈ [1, +∞), M ∈ [0, +∞) (often practically normalized to [0,1+]).

3.2 Interpretive Notes

• Additivity of S and T: Space and time provide independent supportive contributions; additivity prevents over-penalizing when one of them is already high.

• Penalty of D: Dimensional/curvature hostility reduces effective support via division.

• Multiplicative role of M: Without usable matter/energy (M=0), viability collapses to zero regardless of geometry or time.

• Threshold: The model is threshold-based rather than purely probabilistic.

3.3 Consistency Checks (Monotonicity and Edge Cases)

• Monotonicity: ∂L/∂S > 0, ∂L/∂T > 0, ∂L/∂M > 0, ∂L/∂D < 0 (under the normalization choices below).

• Edge cases:

  • M = 0 ⇒ L = 0.

  • D → ∞ ⇒ L → 0.

  • S = T = 0 ⇒ L = 0 even if M > 0.

  • S,T near 1 with moderate D and M above critical ⇒ L high.

Variable Definitions (with Representative Measurable Forms) Note: Forms below are representative examples to demonstrate measurability; each can be recalibrated with data.

4.1 Space Support (S) Definition: Degree to which spatial conditions support life. Representative formulation: S = [ r_h / ( |r − r_h| + epsilon ) ] * g_s where r = orbital radius, r_h = optimal habitable-zone radius for the star class, g_s = gravitational/atmospheric retention stability factor (0–1), epsilon = small regularization constant. Range: 0 ≤ S ≤ 1.

4.2 Time Stability (T) Definition: Duration and reliability of supportive conditions. Representative formulation: T = (Δt / Δt_crit) exp(−E_dot Δt) where Δt = duration of stable conditions (years), Δt_crit = minimum critical window for life emergence (e.g., 1e8 years), E_dot = normalized entropy-acceleration or destabilization rate. Range: 0 ≤ T ≤ 1 (capped at 1 after normalization).

4.3 Dimensional Cost (D) Definition: Penalty factor for curvature/instability. Representative formulation: D = 1 + kappa + Lambda + xi where kappa = normalized spacetime curvature penalty (e.g., compact-object proximity, tidal shear index), Lambda = normalized cosmological constant contribution where applicable, xi = additional dimensional instability factor (0 if absent). Range: D ≥ 1; larger D decreases L.

4.4 Matter–Energy Presence (M) Definition: Density and accessibility of usable matter/energy to drive life processes. Representative formulation: M = (rho Z) / (rho_crit Z_crit) where rho = usable energy density or flux (e.g., W/m^2 or J/m^3 mapped to a normalized scale), Z = elemental/chemical availability index (with emphasis on bio-essential elements and solvents), and rho_crit, Z_crit are critical baselines. Range: M ≥ 0 (often normalized to ~0–1+ with practical caps).

4.5 Life Viability Function (L) L = ((S + T) / D) * M Threshold: L >= L_critical (empirical constant; initial planetary-scale estimate in the 0.1–0.2 range to be refined by calibration).

Comparative Analysis

5.1 Positioning vs. Einstein’s Field Equations (GR)

• Domain: GR relates spacetime geometry to energy–momentum. MARR is not a dynamical spacetime equation; it is a viability index.

• Structural role: D distills curvature/instability into a scalar penalty derived from GR context (e.g., tidal forces, radiation hazards).

• Complementarity: GR quantifies geometry; MARR asks whether that geometry plus other factors crosses a life threshold.

5.2 Positioning vs. the Drake Equation

• Drake estimates the expected number of communicative civilizations via multiplicative probabilities.

• MARR yields a local viability index L for emergence/sustainment (not communications) with a binary threshold L >= L_critical.

• Structural difference: Additive supports (S+T), divisive penalty (D), multiplicative availability gate (M).

5.3 Thermodynamics and Free-Energy Framing

• M encodes usable free energy and material availability.

• T penalizes high entropy acceleration via exp(−E_dot * Δt).

• Environments with sustained gradients and moderate entropy production tend to raise L.

5.4 Habitability Metrics (HZ/CHZ, Stellar Stability)

• Existing indices map into S (placement/stability) and T (duration/continuity).

• MARR unifies those indices with D and M in a single criterion.

5.5 Quantum/Temporal Considerations

• T includes temporal coherence and stability of causal structure.

• D increases when exotic curvature or indefinite causal order plausibly induces macroscopic instability.

• The framework is agnostic; only measured or well-motivated penalties/benefits should alter T or D.

5.6 Why (S + T), Why Divide by D, Why Multiply by M

• Add S and T: independent supports; neither fully substitutes for the other.

• Divide by D: environmental/metric hostility reduces net support.

• Multiply by M: zero resources implies zero viability.

5.7 Identifiability and Calibration Path

• Normalize S, T to [0,1]; set D ≥ 1; map M to [0,1+] with caps.

• Anchors:

  • S: insolation fraction of optimal × gravitational/atmospheric retention score.

  • T: fraction of time above habitability minima across Δt, discounted by hazard rates.

  • D: monotone transform of curvature/instability proxies (tidal shear, radiation, compact-object indices).

  • M: normalized free-energy flux × bio-essential abundance relative to critical baselines.

• Fit L_critical using retrospective cases (Earth-like epochs vs. sterile analogs), then validate prospectively on exoplanets.

5.8 Failure Modes and Falsifiability

• If environments with L << L_critical later show robust life: mis-estimated parameters or missing interactions; revise forms/calibrations.

• If environments with L >> L_critical remain sterile after exhaustive search: reassess thresholds or add cross-terms.

5.9 Optional Extensions (kept out of v1.0 core)

• Interaction term: L = [ (S + T + αST) / D ] * M (α >= 0) for synergy.

• Saturation of M: replace M with sigmoid σ(M) = 1 / (1 + exp(−β(M − M0))) to avoid unbounded boosts.

• Risk channels: Decompose D = 1 + κ + Λ + ξ + R_rad + R_tidal + … for attribution.

Applications

6.1 Cosmology and Exoplanet Viability Apply MARR to exoplanet catalogs: S (orbit, stability), T (stellar/planetary continuity), D (curvature/radiation penalties), M (resources). Screen candidates beyond insolation alone.

6.2 Astrobiology and Origins of Life Abiogenesis requires L >= L_critical. Early Earth as calibration (high M, high T); Mars as an example where T later collapsed.

6.3 Quantum and Dimensional Modeling Assess whether causal stability and geometric regularity allow coherent life processes (T, D adjustments).

6.4 Artificial Intelligence and Simulated Universes Map S to structural fidelity, T to runtime stability, D to computational instability/overhead, M to resource allocation. Extends viability assessment to synthetic domains.

6.5 Cross-Disciplinary Integration Astronomy (screening), Biology (abiogenesis constraints), Physics (GR/thermo/quantum bridge), Engineering (closed habitats).

Case Studies / Examples (Illustrative Normalizations)

7.1 Earth (Baseline) S ≈ 0.95; T ≈ 0.90; D ≈ 1.00; M ≈ 1.00 L = ((0.95 + 0.90) / 1.00) * 1.00 = 1.85 >> L_critical

7.2 Mars (Marginal) S ≈ 0.60; T ≈ 0.20; D ≈ 1.00; M ≈ 0.40 L = ((0.60 + 0.20) / 1.00) * 0.40 = 0.32 ≳/≲ threshold briefly, then below as T collapses

7.3 Proxima Centauri b (Hypothetical) S ≈ 0.70; T ≈ 0.50; D ≈ 1.50; M ≈ 0.60 L ≈ ((0.70 + 0.50) / 1.50) * 0.60 ≈ 0.48 borderline, contingent on atmospheric retention

Discussion

8.1 Strengths

• Unified structure across space, time, dimensional penalty, and resources.

• Threshold criterion enables falsifiable predictions.

• Extensible as data improve.

• Cross-domain applicability (cosmic to synthetic).

8.2 Challenges

• Parameterization of S, T, D, M requires rigorous, data-driven normalization.

• Calibration of L_critical across broader datasets.

• Possible nonlinear interactions (e.g., S↔T coupling) may warrant cross-terms.

• Empirical measures for D are sparse; need robust proxies.

• Anthropocentric bias from Earth-centric calibration.

8.3 Future Directions

• Apply to large exoplanet catalogs with current stellar/planet parameters.

• Integrate into climate/geophysical simulations for stress-testing.

• Comparative planetology beyond Earth/Mars (Venus, Europa, Enceladus, Titan).

• Explore behavior of T and D under non-classical temporal/geom. regimes.

• Evaluate in synthetic closed-loop habitats and computational worlds.

8.4 Broader Implications MARR reframes life viability as a balance of space, time, dimensional penalty, and resource sufficiency—a testable, integrative index connecting physics and biology.

Conclusion

The MARR Equation provides a unified, threshold-based model for life viability:

L = ((S + T) / D) * M

It integrates space, time, dimensional penalties, and matter–energy sufficiency into a single framework. Case studies show consistency with observed planetary outcomes. Designed to be falsifiable and extensible, MARR offers a foundation for cross-disciplinary exploration of life’s conditions at planetary, cosmological, and synthetic scales.

References (Two Sets)

A) Lean Core References (suitable for immediate IP lock)

• Drake, F. D. (1961). Project Ozma. Physics Today, 14(4), 40–46.

• Einstein, A. (1916). The foundation of the general theory of relativity. Annalen der Physik, 49(7), 769–822.

• Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. (1993). Habitable zones around main sequence stars. Icarus, 101(1), 108–128.

• Lanza, R. (2009). Biocentrism. BenBella Books.

• Lingam, M., & Loeb, A. (2019). Life in the cosmos. Harvard University Press.

• Lloyd, S. (2000). Ultimate physical limits to computation. Nature, 406, 1047–1054.

• Milner, S., et al. (2019). Quantum switch and indefinite causal order. Nature Communications, 10, 3020.

• Sagan, C. (1994). Pale blue dot. Random House.

• Ward, P. D., & Brownlee, D. (2000). Rare Earth. Copernicus.

B) Expanded References (journal-ready breadth)

• Drake, F. D. (1961). Project Ozma. Physics Today, 14(4), 40–46.

• Einstein, A. (1916). The foundation of the general theory of relativity. Annalen der Physik, 49(7), 769–822.

• England, J. L. (2013). Statistical physics of self-replication. J. Chem. Phys., 139(12), 121923.

• Hardy, L. (2001). Quantum theory from five reasonable axioms. arXiv:quant-ph/0101012.

• Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. (1993). Habitable zones around main sequence stars. Icarus, 101(1), 108–128.

• Lanza, R. (2009). Biocentrism. BenBella Books.

• Lingam, M., & Loeb, A. (2019). Life in the cosmos. Harvard University Press.

• Lloyd, S. (2000). Ultimate physical limits to computation. Nature, 406, 1047–1054.

• Milner, S., et al. (2019). Quantum switch and indefinite causal order. Nature Communications, 10, 3020.

• Orgel, L. E. (1998). The origin of life—A review of facts and speculations. Trends Biochem. Sci., 23(12), 491–495.

• Oreshkov, O., Costa, F., & Brukner, Č. (2012). Quantum correlations with no causal order. Nature Communications, 3, 1092.

• Prigogine, I., & Stengers, I. (1984). Order out of chaos. Bantam.

• Sagan, C. (1994). Pale blue dot. Random House.

• Schrödinger, E. (1944). What is life? Cambridge University Press.

• Seager, S., Bains, W., & Hu, R. (2013). Biosignature gases in H2-dominated atmospheres on rocky exoplanets. ApJ, 777(2), 95.

• Szostak, J. W., Bartel, D. P., & Luisi, P. L. (2001). Synthesizing life. Nature, 409(6818), 387–390.

• Ward, P. D., & Brownlee, D. (2000). Rare Earth. Copernicus.

• Zeng, L., Sasselov, D. D., & Jacobsen, S. B. (2019). Mass–radius relation for rocky planets (PREM). ApJ, 870(2), 113.

• Zuckerman, B. (2019). Habitable planets are rare: Life after Kepler. PASP, 131(1003), 072001.